Динамическое рассеяние света

(другие названия данного метода: фотонная корреляционная спектроскопия; квазиупругое рассеяние света)

Для измерения размеров наночастиц используется метод динамического рассеяния света (ДРС). Данный метод позволяет определить коэффициент диффузии дисперсных частиц в жидкости путем анализа корреляционной функции флуктуаций интенсивности рассеянного света. Далее, из коэффициента диффузии рассчитывается радиус наночастиц.

Основные идеи метода динамического рассеяния света

• Броуновское движение дисперсных частиц или макромолекул в жидкости приводит к флуктуациям локальной концентрации частиц. Результатом этого являются локальные неоднородности показателя преломления и соответственно - флуктуации интенсивности рассеянного света при прохождении лазерного луча через такую среду.
• Коэффициент диффузии частиц обратно пропорционален характерному времени релаксации флуктуаций интенсивности рассеянного света. Это характерное время, в свою очередь, есть время затухания экспоненциальной временной корреляционной функции рассеянного света, которая измеряется с помощью цифрового коррелятора.
• Размер частиц (гидродинамический радиус) рассчитывается по формуле Стокса-Эйнштейна, которая связывает размер частиц с их коэффициентом диффузии и вязкостью жидкости.

Метод динамического рассеяния света используется также для измерения скоростей потоков жидкостей и газов. Традиционно, этот вариант метода носит название лазерной доплеровской анемометрии (ЛДА). В частности, данная конфигурация метода ДРС используется для измерения электрофоретической подвижности наночастиц, откуда рассчитывается их дзета-потенциал.

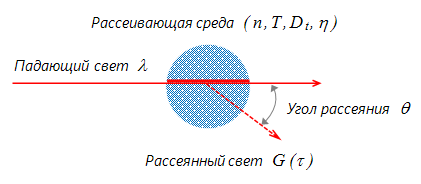
В качестве примера рассмотрим диффузию монодисперсных наночастиц, диспергированных в жидкости. Хаотическое броуновское движение дисперсных частиц приводит к микроскопическим флуктуациям их локальной концентрации и соответствующим локальным неоднородностям показателя преломления среды. При прохождении лазерного луча через такую среду часть света будет рассеяна на этих неоднородностях. Флуктуации интенсивности рассеянного света будут соответствовать флуктуациям локальной концентрации дисперсных частиц. Информация о коэффициенте диффузии частиц содержится в зависящей от времени корреляционной функции флуктуаций интенсивности. Временная автокорреляционная функция согласно определению имеет следующий вид:

$$ G(\tau) = \langle I(0)I(t-\tau) \rangle = \lim_{t_m \rightarrow\infty}\frac1{t_m}\int_{0}^{t_m}I(t)I(t-\tau)\partial t $$

где интенсивность I имеет различные значения во время t и (t-τ). t_m - это время интегрирования (время накопления корреляционной функции). Очевидно, что при τ = 0, автокорреляционная функция равна среднеквадратичной интенсивности рассеяния <I ²>. Для бесконечного времени корреляция отсутствует, и автокорреляционная функция равна квадрату средней интенсивности рассеяния:

$$ G(\tau) = \langle I(0)I(t-\tau) \rangle = \langle I(0) \rangle \langle I(t-\tau) \rangle = \langle I \rangle ^2 $$

В соответствии с гипотезой Онзагера, релаксация микроскопических флуктуаций концентрации к равновесному состоянию может быть описана первым законом Фика (уравнением диффузии):

$$ \frac{\partial c(\overrightarrow{r},t)}{\partial t} = -D \triangledown c(\overrightarrow{r},t) $$

где c(r, t) - концентрация и D - коэффициент диффузии частиц. Можно показать, что в такой системе автокорреляционная функция интенсивности рассеяния света экспоненциально затухает во времени, и характерное время релаксации однозначно связано с D. Корреляционная функция интенсивности рассеянного света (для случая квадратичного детектирования) имеет вид:

$$ G(\tau) = a \exp \left(\frac{-2 \tau}{t_c}\right) + b $$

где в соответствии с решением уравнения диффузии обратное время корреляции равно:

$$ \frac{1}{t_c} = D_t q^2 $$

Волновой вектор флуктуаций концентрации описывается выражением:

$$ q = \frac{4\pi n}{\lambda} \sin \left(\frac{\theta}{2}\right) $$

В выражениях 4-6: a и b - экспериментальные константы, n- показатель преломления жидкости, в которой взвешены дисперсные частицы,λ - длина волны лазерного света и θ - угол рассеяния.

Схема процесса рассеяния света

 

Автокорреляционная функция рассеянного света

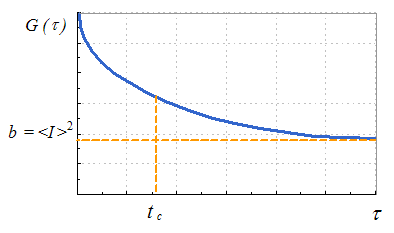
Величины t_c, a и b могут быть найдены путем аппроксимации измеренной корреляционной функции теоретической экспоненциальной функцией. Для сферических невзаимодействующих между собой частиц размер их может быть рассчитан с использованием формулы Стокса-Эйнштейна:

$$ D = \frac{k_bT}{6\pi \eta R} $$

где k_B - константа Больцмана, T - абсолютная температура и η - сдвиговая вязкость среды, в которой взвешены частицы радиуса R.

Из формулы Стокса-Эйнштейна понятно, что с помощью динамического рассеяния света можно решать задачи измерения вязкости жидкости. Для случая рассеяния света на дисперсных частицах известного размера, измеренное характерное время флуктуаций позволяет рассчитать вязкость жидкости. Причем в данном случае можно говорить о микрореологической вязкости, которая, в принципе, может отличаться от вязкости, измеренной на макроскопических масштабах.

Проблема аппроксимации экспериментальных данных проста для рассмотренного случая рассеяния света монодисперсными сферическими частицами. Для полидисперсных образцов интерпретация экспериментальных данных усложняется. Для реально достижимой точности измерений могут быть получены только два-три параметра одномодального полидисперсного распределения: средний размер частиц, ширина и асимметрия распределения. Для многомодальных полидисперсных систем можно говорить о средних размерах частиц каждой компоненты и относительном вкладе каждой компоненты в интенсивность рассеяния. Важно отметить, что два близких размера частиц полидисперсной системы будут разрешаться в виде отдельных компонент только, если их размеры отличаются друг от друга не менее, чем в 2-3 раза.